正则化
正则化
1.基本公式
经验风险最小化:$min{1\over N}\sum\limits_{i=1}^NL(y_i,f(x_i))$
正则化项:$\lambda J(f)$
L1正则化项:$||w_1||=|w1|+|w2|+…..+|w_n|$
L2正则化项:$||w_2||=\sqrt [2]{w_1^2+w_2^2+…..+w_n^2}$
结构风险最小化:$min{1\over N}\sum_{i=1}^{N}L(y_i,f(x_i)+\lambda J(f)$
注:其中λ 是正则化参数,用来控制正则化项在整体损失函数中的重要程度。较大的 λ 值会增加对模型复杂度的惩罚,从而更强调正则化的效果。
2.基本概念
过拟合:模型过于复杂或过度拟合了训练数据的细节和噪声,导致对新数据的泛化能力不佳。
欠拟合:无法在训练数据上达到较好的拟合效果,也不能很好地泛化到新数据。
正则化:在经验风险的基础上增添了一个正则化项,用来控制模型的复杂度,可以防止过拟合。通过正则化可以选择出经验风险和模型复杂度同时较小的模型。
3.常见问题:
3.1为什么正则化可以防止过拟合?
答:正则化等价于对模型的复杂度添加约束条件,其具有相同的解空间。
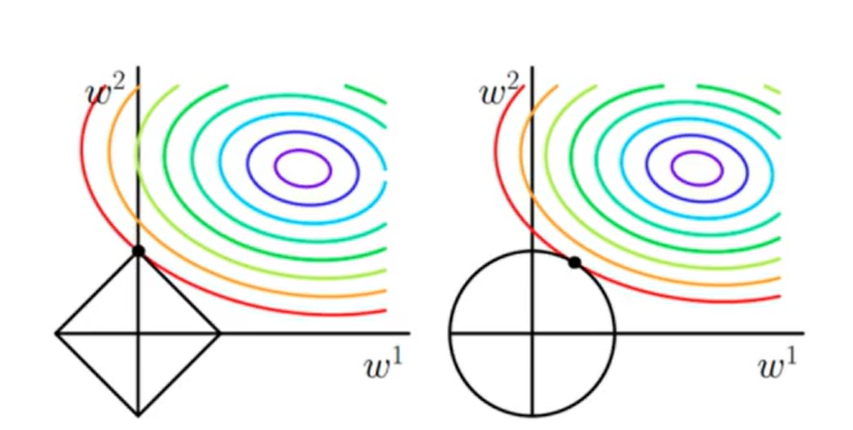
3.2为什么L1正则化具有稀疏性?
答:在最小化损失函数时,L1正则化项会与损失函数一起构成优化问题。从解空间形状的角度分析,,另外,L1正则化在参数空间中形成了一个尖锐的角,使得优化算法更有可能选择参数为零的解(即L1正则化图像与损失函数的等值线的交点更可能位于坐标轴上)。
从贝叶斯的观点,所有的正则化都是来自于对参数分布的先验,Laplace先验会导出L1正则化,Gauss先验会导出L2正则化,而Laplace分布取零值的概率较大,所以参数取零值的概率较大,因而L1正则化具有稀疏性。
3.3推导L1先验分布是Laplace分布
后验概率:$P(\theta|D)={P(D|\theta)*P(\theta)} \over P(D) $
要使后验概率最大,即使$P(D|\theta)*P(\theta)$最大
取log加负号后求其最小值:
其等价于求$-\sum\limits_{i=1}^NlogP(x_i|\theta)-log(P(\theta))$的最小值
假设$P(\theta)$满足拉普拉斯分布:
代入$P(\theta)$后,即求$-\sum\limits_{i=1}^NlogP(x_i|\theta)-log({1 \over {2\lambda}})+{1 \over \lambda}|\theta|$
其相当于L1正则