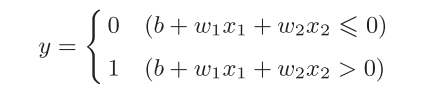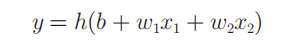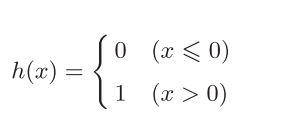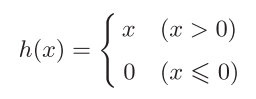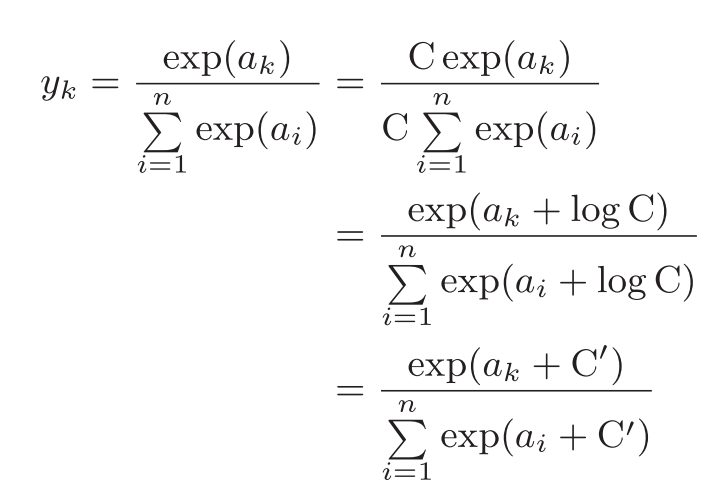神经网络

1. 激活函数

激活函数：作用在于决定如何来激活输入信号的总和。

如，感知机的数学形式：img2

其亦可表达为：

img3

img4

h(x)函数会将输入信号的总和转换为输出信号，即为激活函数。

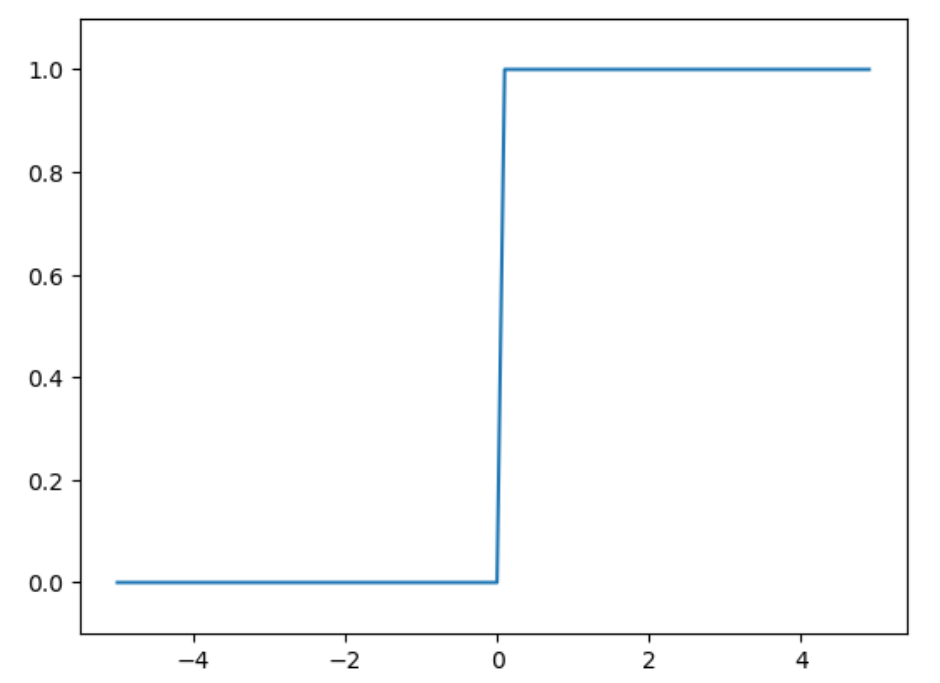
1.1 阶跃函数

激活函数：以阈值为界，一旦输入超过阈值，就切换输出。

1
2
3
4
5
#当输入超过0时，输出1，否则输出0的阶跃函数
def step_function(x):
  y = x > 0
  return y.astype(np.int)
  #用astype()方法转换NumPy数组的类型

阶跃函数的图形

1
2
3
4
5
6
7
8
9
import numpy as np
import matplotlib.pylab as plt
def step_function(x):
 return np.array(x > 0, dtype=np.int)
x = np.arange(-5.0, 5.0, 0.1)
y = step_function(x)
plt.plot(x, y)
plt.ylim(-0.1, 1.1) # 指定y轴的范围
plt.show()

img5

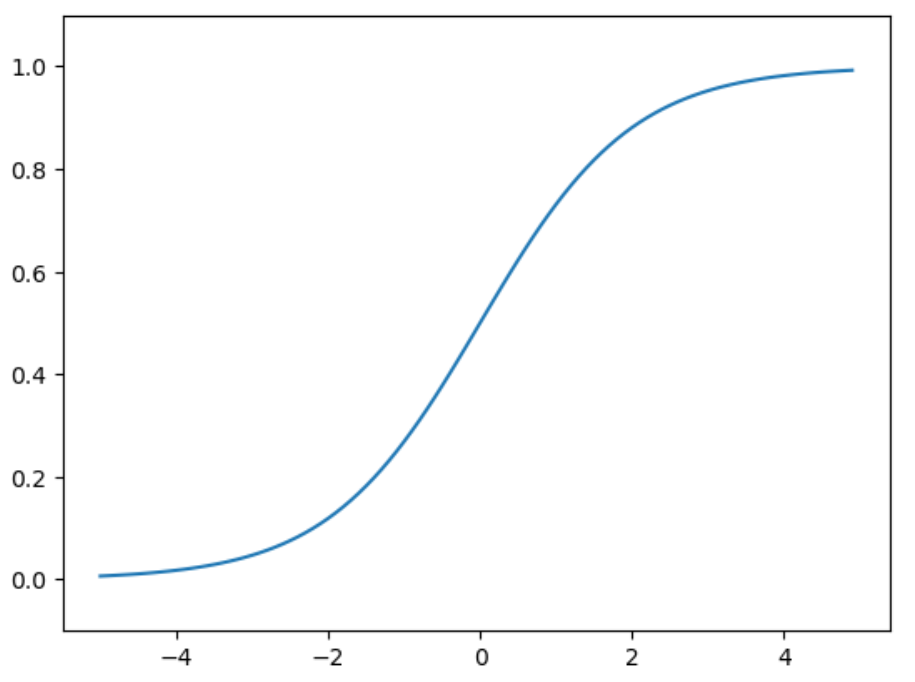
1.2 sigmoid函数

sigmoid函数: $h(x)={1 \over 1+e^{-x} }$

1
2
def sigmoid(x):
 return 1 / (1 + np.exp(-x))

sigmoid函数的图形

1
2
3
4
5
x = np.arange(-5.0, 5.0, 0.1)
y = sigmoid(x)
plt.plot(x, y)
plt.ylim(-0.1, 1.1) # 指定y轴的范围
plt.show()

​ img6

注：神经网络的激活函数必须使用非线性函数。使用线性函数时，加深神经网络的层数就没有意义了，因为不管如何加深层数，总是存在与之等效的“无隐藏层的神经网络”。

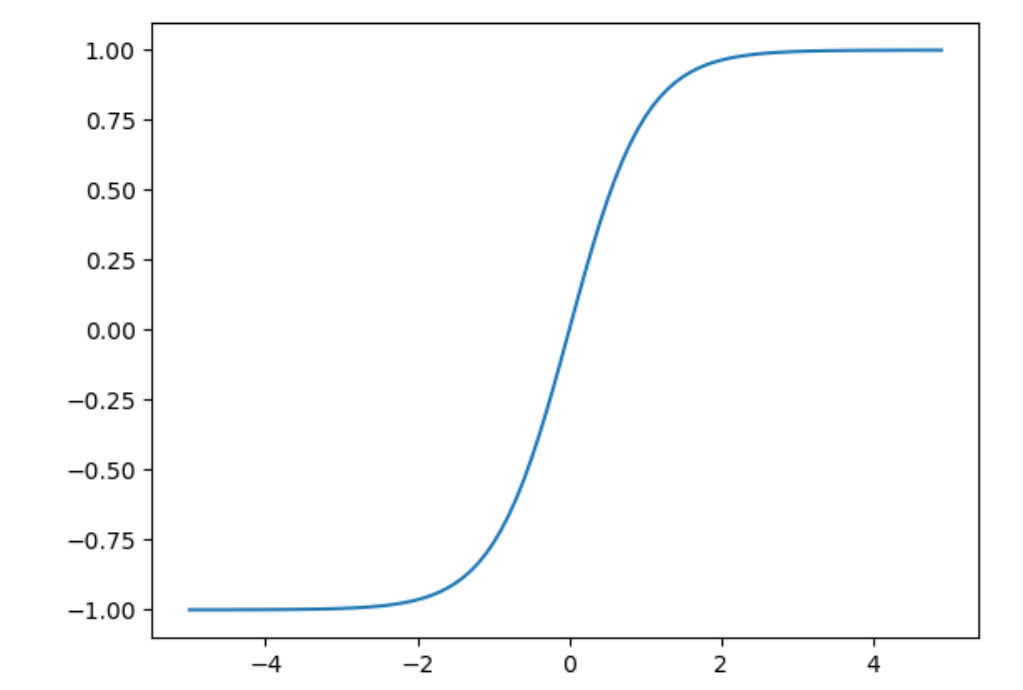
1.3 tanh函数

tanh函数：$\LARGE {e^{x}-e^{-x}\over e^{x}+e^{-x} }$

img11

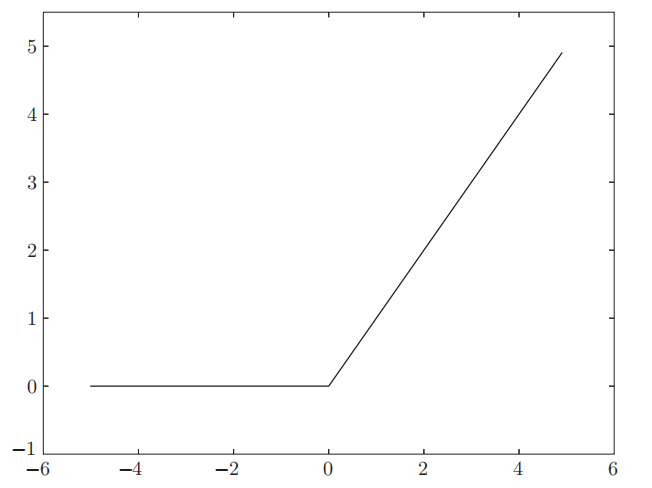
1.4 ReLU函数

ReLU函数：img7

1
2
def relu(x):
 return np.maximum(0, x)

ReLU函数的图形

img8

Leaky ReLU函数:max(0.1x,x)

2 恒等函数和 softmax函数

恒等函数：将输入按原样输出，对于输入的信息，不加以任何改动地直接输出。

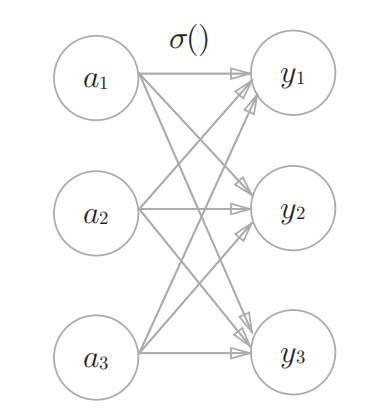
softmax函数：

为了防止溢出，可对softmax函数进行如下改进：

img10

注：其中，$C^{，}$通常使用输入信号中的最大值，来防止溢出。

img9

注：

1.softmax函数的输出通过箭头与所有的输入信号相连，输出层的各个神经元都受到所有输入信号的影响。

2.softmax函数将输出的给类别的得分转换成了概率

3. 交叉熵损失

交叉熵损失：用于比较分类器预测分布与真实分布的距离。

熵：H(p)=$-\sum p(x)log(p(x))$

交叉熵：H(p,q)=$-\sum p(x)log(q(x))$

相对熵(KL散度)：KL(p||q)=$-\sum p(x)log({q(x)\over p(x)})$

三者之间的关系：H(p,q)=KL(p||q)+H(p)

p(x):真实分布概率 q(x):分类器预测分布概率

注：

1.相对熵(KL散度)用于度量两个分布间的不相似性。

2.真实分布为one-hot形式时，H(p)=0,用H(p,q)代替KL(p||q),且交叉熵损失可化简为L=$-log(q_j)$,其中j为真实的类别。

3. 参数优化

参数优化：利用损失函数的输出值作为反馈信号来调整分类器的参数。

3.1 梯度下降算法

原理：对于最小化优化问题，只需要将参数沿着梯度相反的方向前进一个步长，就可以实现目标函数的下降。

方向：负梯度方向

移动：步长(学习率)

随机梯度下降算法：每次随机选择一个样本，计算损失并更新梯度。

缺点：单个样本的训练易受噪声的影响，不是每次迭代都向着整体最优化的方向。

小批量随机梯度下降：每次选择m个样本，计算损失并更新梯度。

3.2 梯度消失与梯度爆炸

梯度消失：由于链式法则的乘法性质导致梯度趋向于0。

注：tanh,sigmoid局部梯度特性不利于网络梯度流的反向传播，尽量选择RelU或Leaky RelU。

梯度爆炸：断崖处梯度乘以学习率后是一个非常大得值，从而“飞”出了合理区域，最终导致算法不收敛;

注：通过限制步长的大小(梯度裁剪)可以避免梯度爆炸。

3.3 梯度下降算法的问题及改进

梯度下降算法的问题：在一个方向上变化迅速而在另一个方向上的变化缓慢，并且通过增大步长不能提高算法的收敛速度。

动量法：利用累加历史梯度信息更新梯度。

步骤：

1.采样

2.计算梯度：g

3.速度更新：v=uv+g(u:动量系数，u=0时为梯度下降算法)

4.更新权值：w=w-$\varepsilon$v($\varepsilon$:学习率）

注：梯度下降算法在局部最小点与鞍点处的梯度为0，无法通过，而动量法由于动量的存在可以通过，可以找到更优的解）

自适应梯度算法(AdaGrad)：减小震荡方向的步长，增大平坦方向的步长。

步骤：

1.采样

2.计算梯度：g

3.累计平方梯度：r=r+g*g (r : 累计变量)

4.更新权值：w=w-${\large \varepsilon \over \sqrt{r}+\delta}*g$($\delta$:小常数，通常取$10^{-5}$,用于防止除0出错）

注：AdaGrad的一个限制是，随着累计变量的不断增大，导致每个参数的步长(学习率)非常小，这可能会大大减慢搜索进度，并且可能意味着无法找到最优值。

RMSProp：累计平方梯度：r=$\rho$r+(1-$\rho$)g*g ($\rho$:衰减系数，通常取0.999)

ADAM:同时使用动量与自适应梯度的思想

步骤：

1.采样

2.计算梯度：g

3.累计梯度：v=uv+(1-u)*g(u:动量系数,通常取0.9)

4.累计平方梯度：r=$\rho$r+(1-$\rho$)g*g

5.修正偏差：$\large \tilde{v}={v\over 1-u^t}$ ,$\large \tilde{r}={r\over 1-\rho^t}$ (t:迭代系数，该步骤极大缓解了算法初期的冷启动的问题)

6.更新权值：w=w-${\large \varepsilon \over \sqrt{\tilde{r}}+\delta}*\tilde{v}$

注：动量法等同于修改学习的“方向”，自适应梯度等同于修改“步长”，ADAM等同于修改“步长”和“方向”。