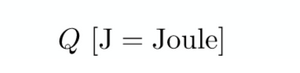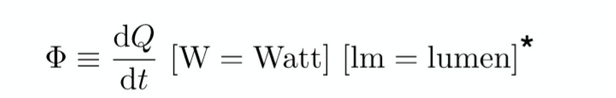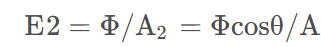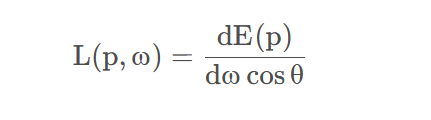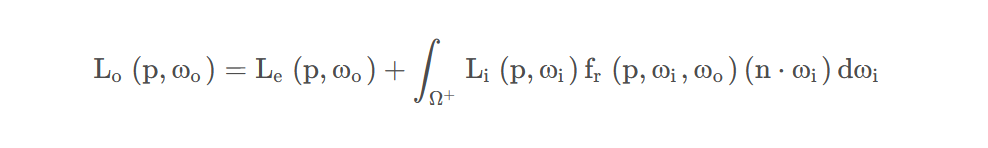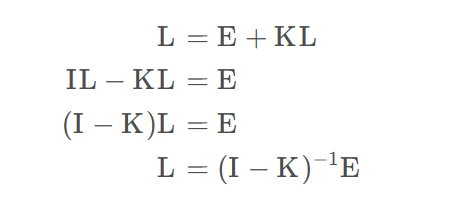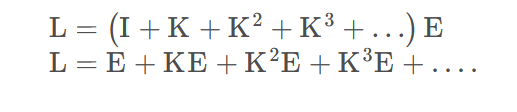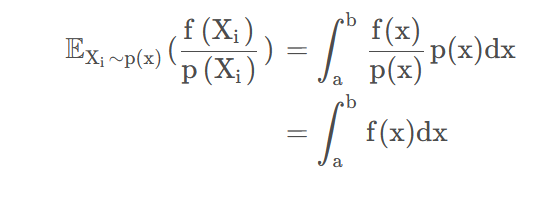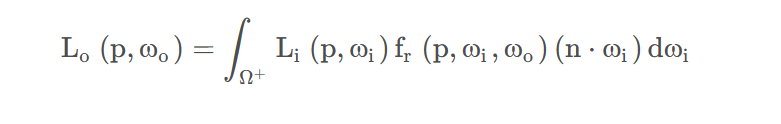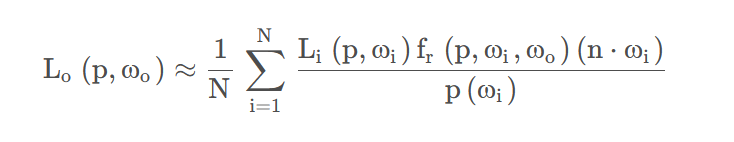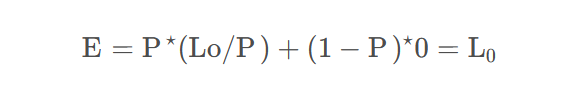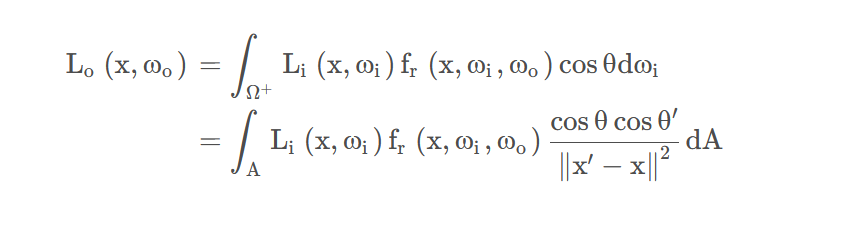辐射度量学
辐射度量学
Whitted-Styled Ray Tracing的缺陷:
- Whitted-Styled Ray Tracing主要关注的是折射光线和反射光线,而没有对漫反射的光线进行追踪。
- 所使用的Blinn-Phong模型是一种简化的模型
因而引入辐射幅度量学来解决此问题。
辐射度量学对光照的一套测量系统和单位,它能够准确的描述光线的物理性质。
1.物理量的定义
1.1. 辐射能量(Radiant energy)和辐射通量(Radiant flux)
辐射能量:描述在一定时间内,通过某个表面或在空间中传播的电磁辐射的总能量量,以焦耳(J)为单位
辐射通量(Radiant Flux):是指光源辐射出的总功率,是在所有方向上的辐射强度的总和,以瓦特(W)为单位
1.2 辐射强度(Radiant intensity)
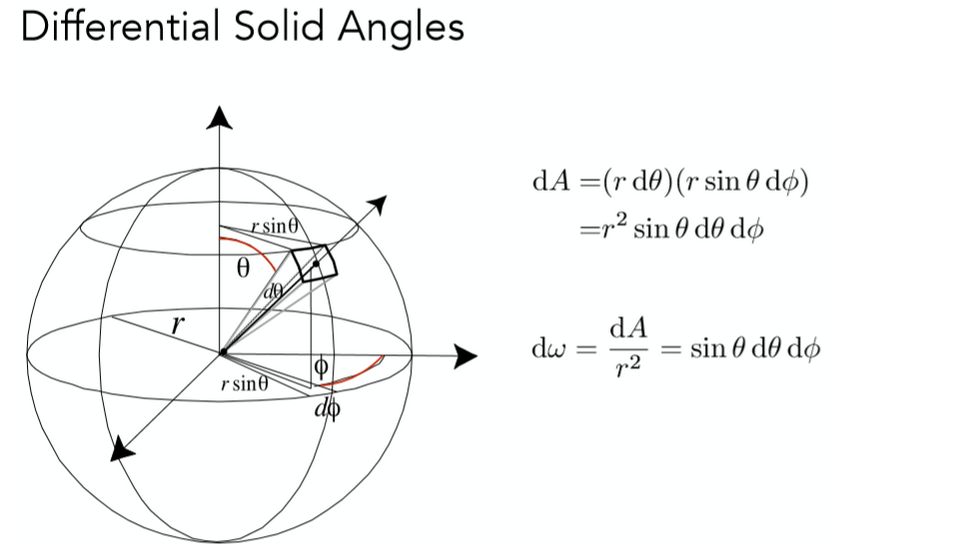
立体角:
注:整个球的立体角为4
微分立体角与和的关系:
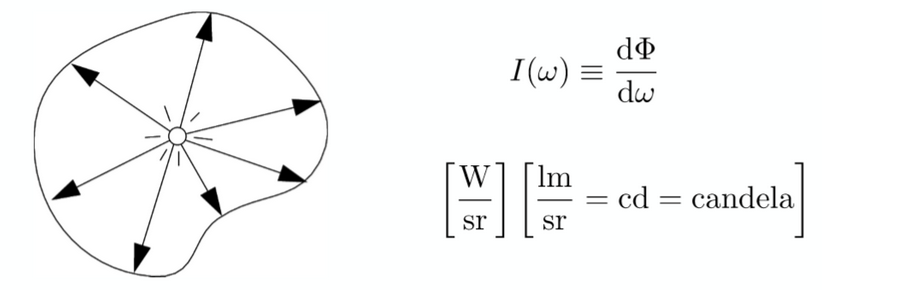
辐射强度(Radiant intensity):光源向特定方向发射的单位立体角内的功率,反映了光源在特定方向上的亮度。
注:辐射强度等于辐射通量除以立体角(各向同性)
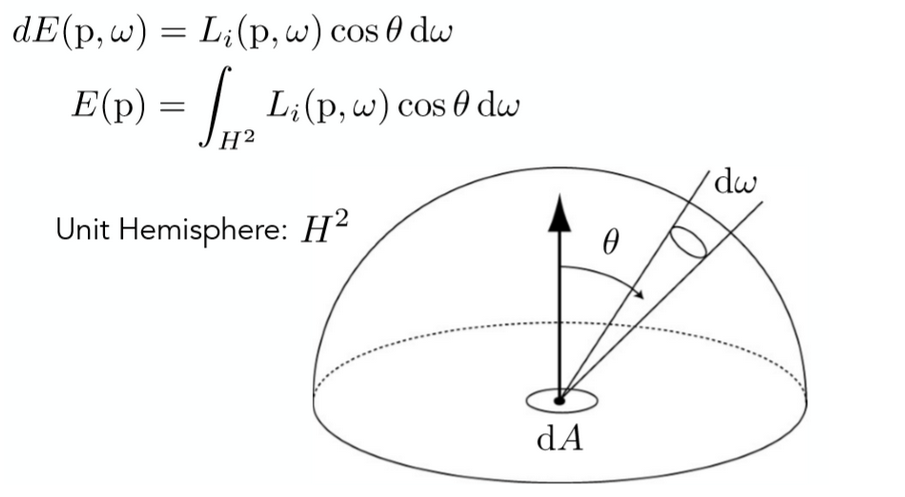
1.3 irradiance
irradiance:每单位照射面积所接收到的光功率
注:当光线斜着照射到平面时,为光线与法线的夹角,该公式变为:
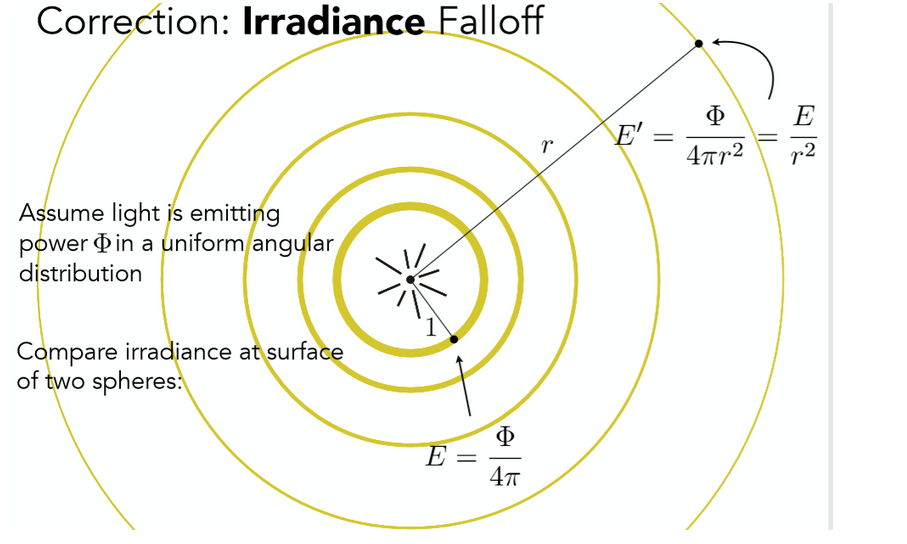
当照射点离光源越远时,A(球的表面积)就越大,irradiance就越小:
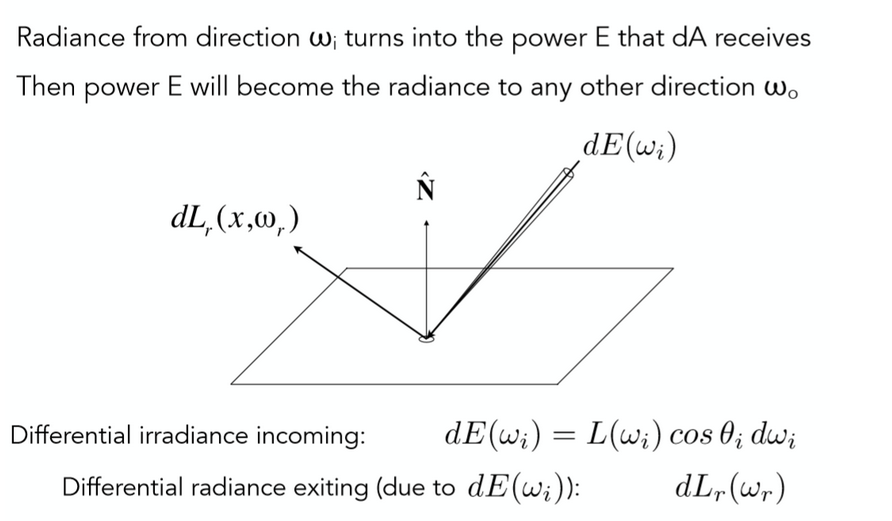
1.4 radiance
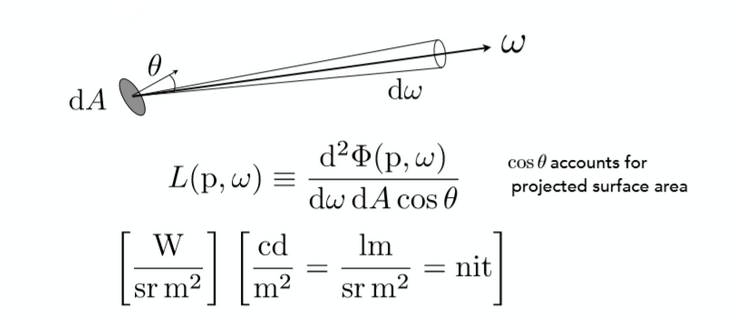
Radiance:每单位立体角、每单位垂直面积的光功率。
注:与irradiance的单位照射面积不同,Radiance定义的是单位垂直面积,二者的关系为:dA⊥=dAcosθ
radiance和irradiance的关系如下:
注:Irradiance是Radiance在整个半球面的立体角上的积累
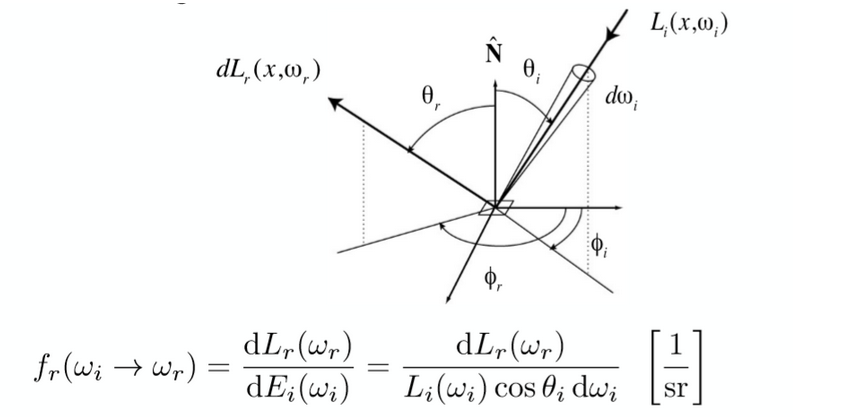
2.双向反射分布函数(BRDF)
空间中的一点(面积微分),在接受到一定方向上的亮度之后,再向不同方向把能量辐射出去
注:能量辐射的过程(即产生的过程)受物体表面材质的影响,如光滑表面会完全反射到镜面反射方向,而粗糙表面会反射到所有方向
BRDF:从特定方向入射的光线经材料表面反射后,沿特定方向散射的相对强度,函数值为反射光的radiance与入射光的irradiance的比值,定义如下:
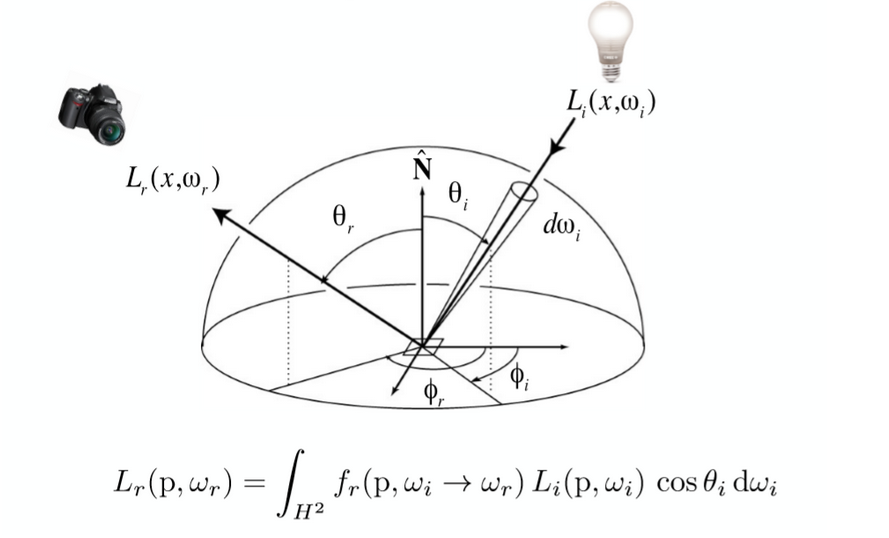
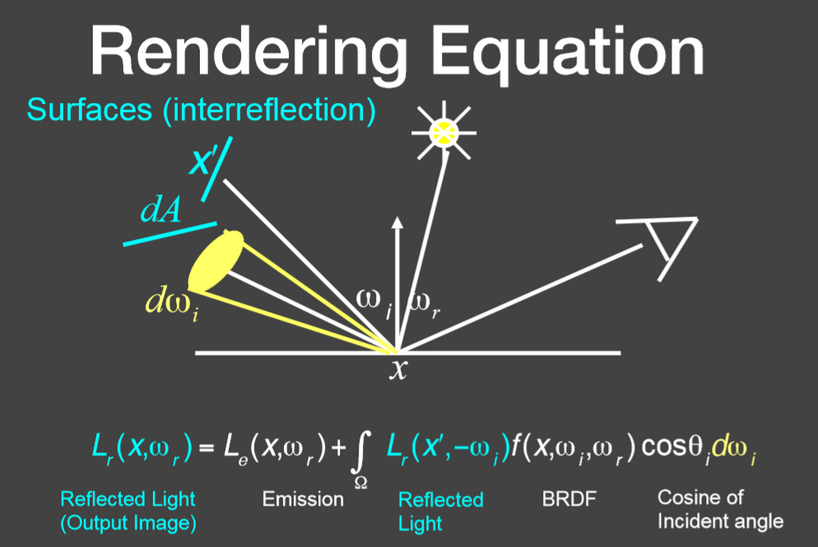
3.反射方程与渲染方程
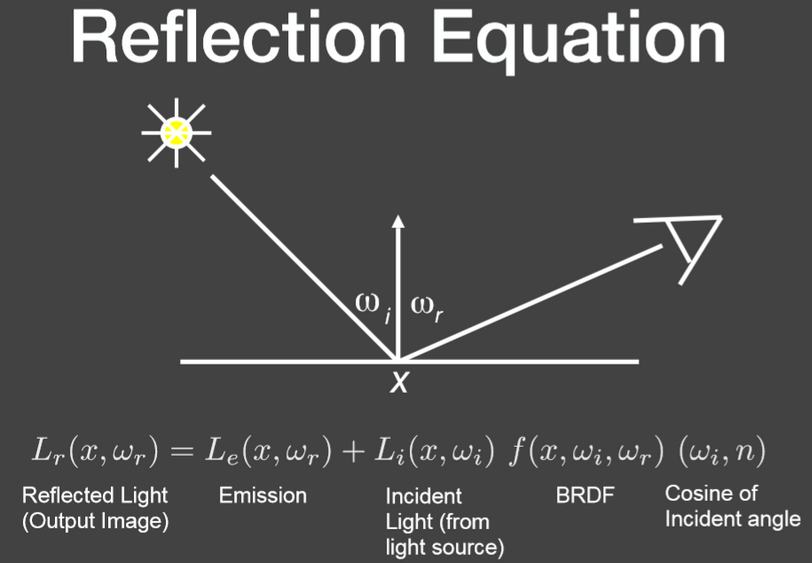
反射方程:
注:
(1).反射光 是由所有不同方向上的入射光线的辐照度 贡献得到的
(2).在相机位置不变的情况下,对于一个固定的表面点p,反射方向 是相对固定的
渲染方程:在反射方程的基础上,增加了一个自发光项
一个点光源和单个物体:
注:点光源对一个点来说自然只有一个方向有入射光
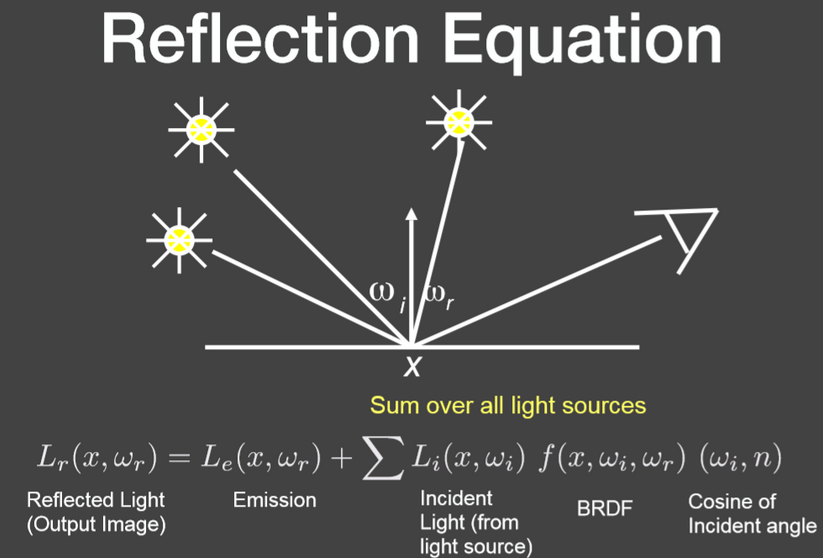
多个点光源一个物体的情况:
注:对多个点光源产生的反射光求和即可
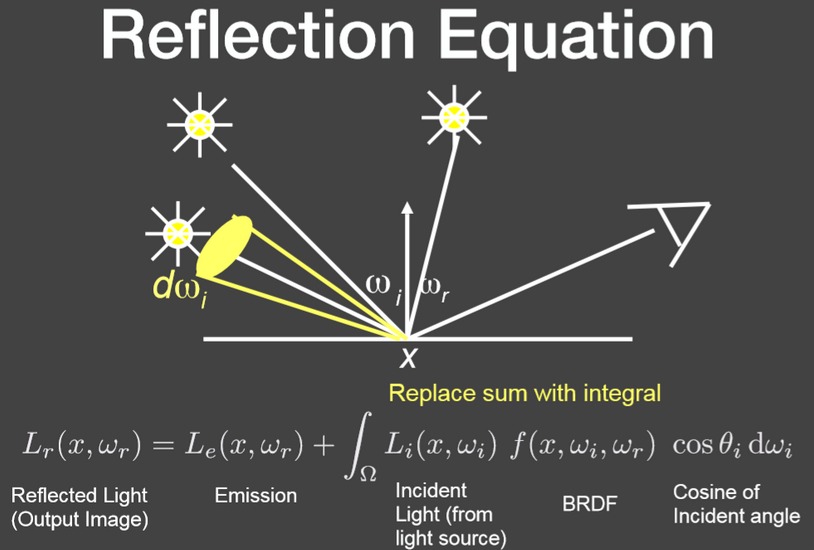
面光源的情况:
注:对面光源所在的立体角的范围积分
考虑场景中其他物体的反射造成的光线交互:
注:将其他物体当作面光源
使用积分变换矩阵可将其写作:L=E+KL
于是得到L:
其中为单位矩阵,再接着对使用广义二项式定理得到:
注:E为自发光项,E+KE为光栅化的结果,即直接光照。对于全局光照,,即一次弹射的间接照明,就是两次弹射的间接照明……
4.蒙特卡洛路径追踪
4.1 蒙特卡洛积分
蒙特卡洛积分:通过对函数进行随机采样来估计积分值的方法,定义如下:
蒙特卡洛的近似正是对积分值的一个无偏估计:
注:蒙特卡洛是一种用来求困难积分的方法
4.2 蒙特卡洛路径追踪
当不考虑自发光项时, 渲染方程:
使用蒙特卡洛积分后:
注:这里取了N个采样方向
只考虑直接光照时,伪代码如下:
加入间接光照后,使用递归的算法,伪代码如下:
注:这时由于使用递归的算法,每次采样N,这会导致指数爆炸的问题
于是,修改N=1,每次只搜索一条路径,重复多次寻找到多条路径,将多条路径的结果求得平均:
注:对经过像素的光线采样多次,而对反射的光线只采样一次
递归出口的设置:RR(俄罗斯轮盘赌)
设定一个概率P,即每次反射有概率P继续递归,递归的返回值为,有(1-P)的概率停止
使用俄罗斯轮盘赌保证了所得到的Radiance的期望不变:
shade函数的伪代码如下:
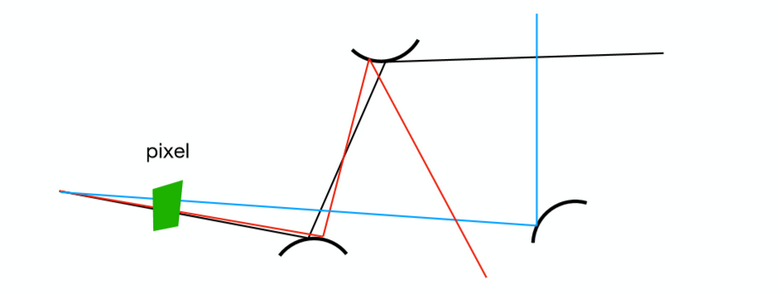
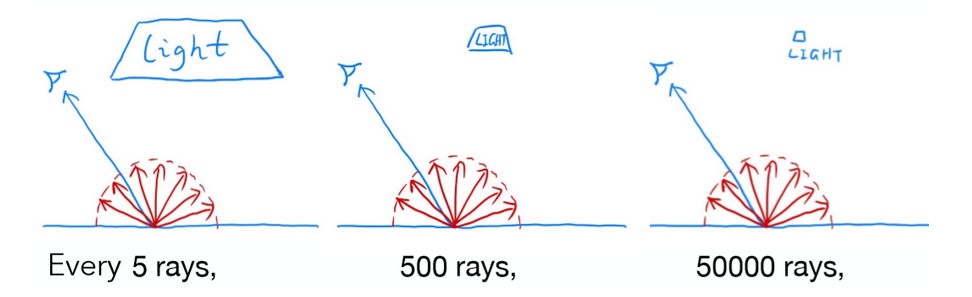
这样的采样,路径追踪效率非常的低下:
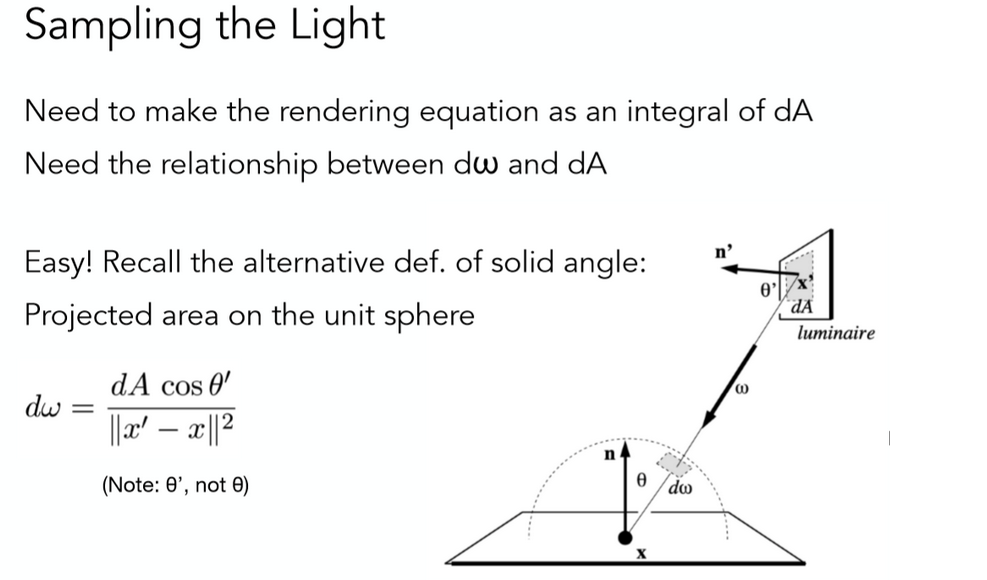
所以,为提高采样的效率,直接对光源进行采样,假设光源的面积为A,dA与的关系如下:
于是渲染方程可改写为:
最终伪代码如下,分直接光照和间接光照两部分计算:
注:在计算直接光照时,要判断光源与着色点之间是否有物体遮挡