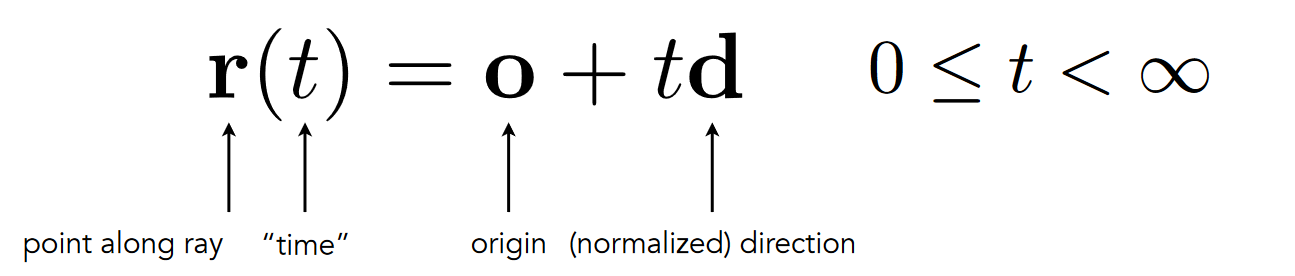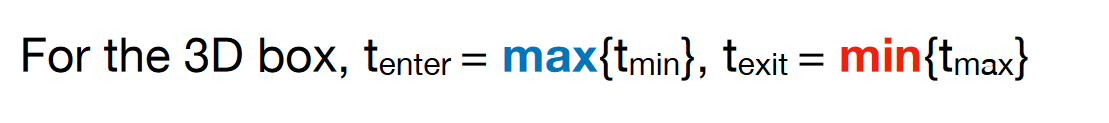1.Shadow Mapping

光栅化的问题：不能很好地表示全局的效果

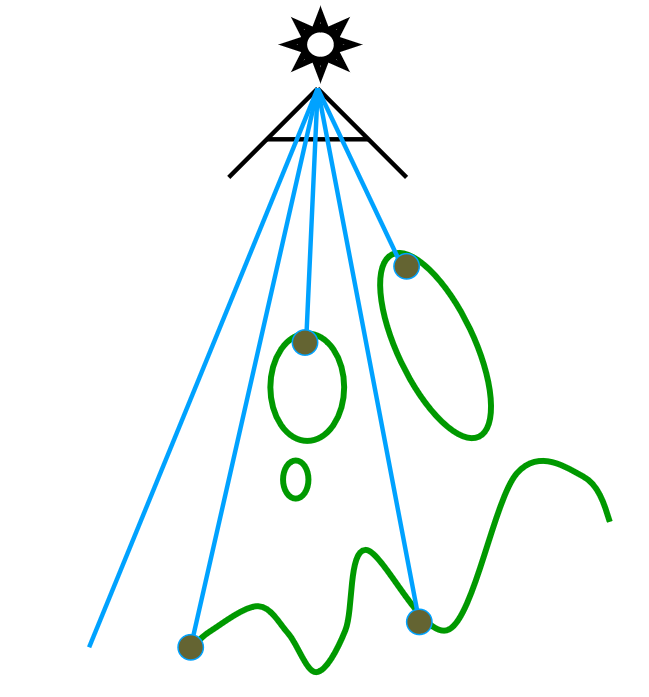
Shadow Mapping： 主要是为了解决点光源的硬阴影的问题

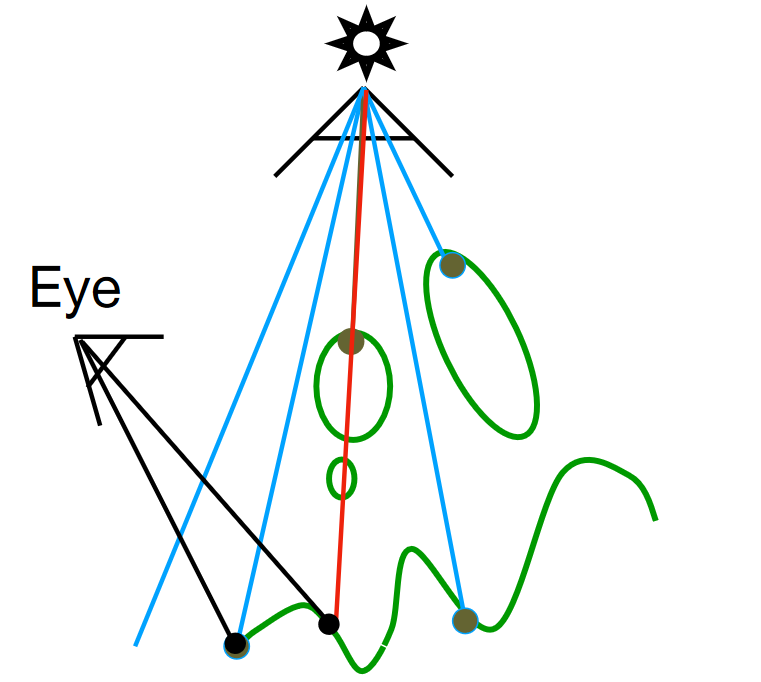
阴影区域：点对相机可见，而对光源不可见

Shadow Map记录每个pixel是否在阴影区域， 其生成步骤如下：

  • 1.从光源位置出发找出可见点，记录光源可见点的深度，得到光源深度图。

    image-20231210115113668

  • 2.从相机出发，找可见点，如果点可见，坐标变换求此点到光源的距离。如果此距离与光源深度图中此位置的深度一致，说明此点可以被光源照到，是为光源、相机能同时看到点；如果不一致，说明是阴影点。

image-20231210115203873

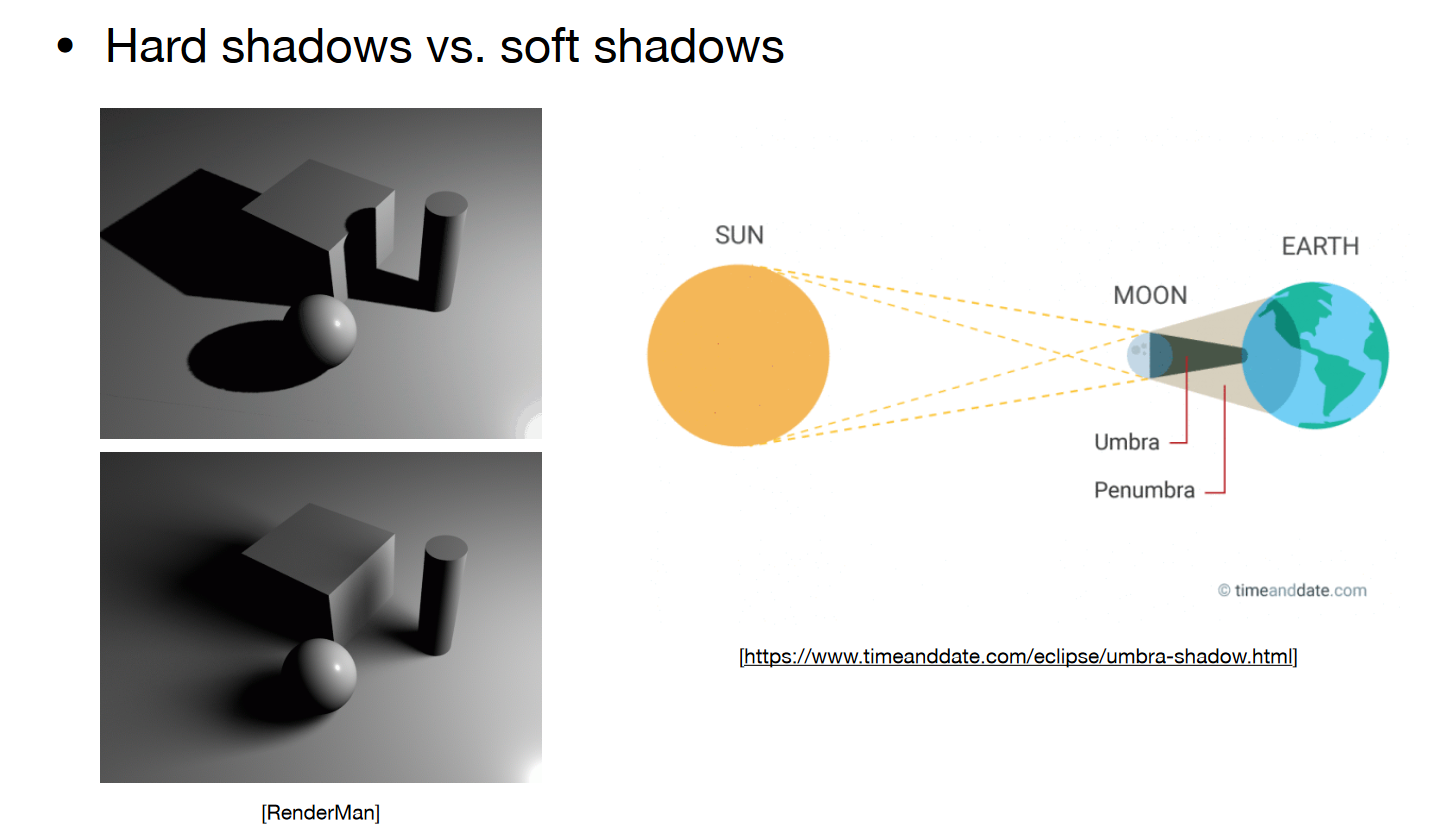
硬阴影与软阴影：

软阴影的形成在于全影和半影的渐变，点光源不存在软阴影问题，出现软阴影一定是光源有大小、不同照射位置有全影和半影这种渐变。

image-20231210120318890

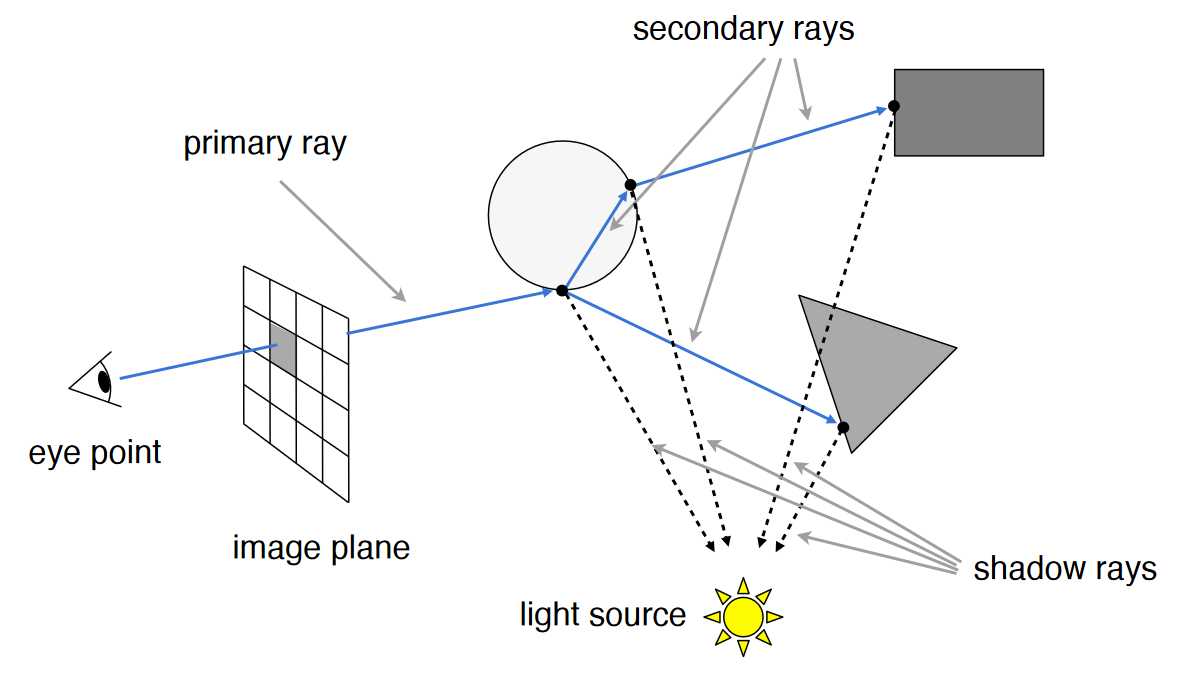
2.Whitted-Styled Ray Tracing

光线追踪利用的就是光的可逆性

利用递归的方法进行光线追踪，对每条光线，递归计算其多个弹射点，当前光线所对应的像素值是由全部弹射点共同决定的：

image-20231210124837928

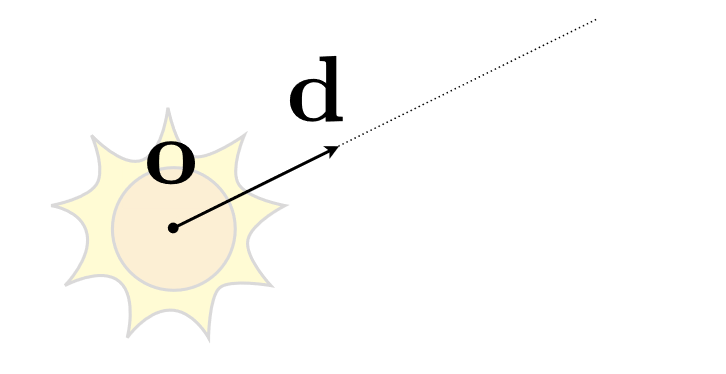
光源的定义：起点+方向

image-20231210124958832

于是，光线上的点可表示为：

image-20231210125038746

3.光线求交点

3.1 隐式表面

隐式表面求交点：将光线上的一点代入隐式方程中求解

image-20231210125547229

3.2 显式表面

显式表面求交点：用光线与三角形求交

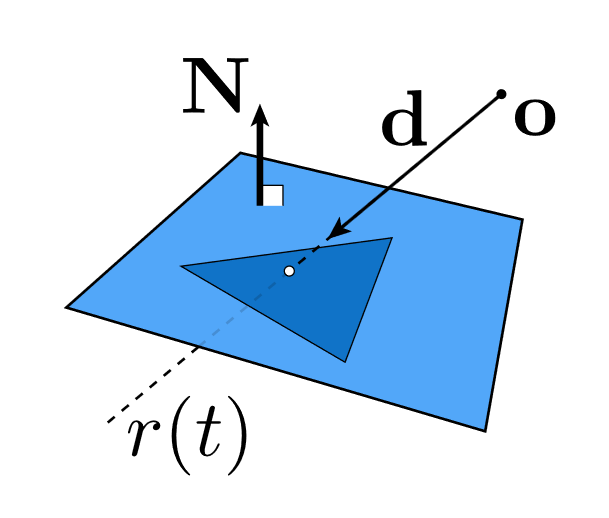
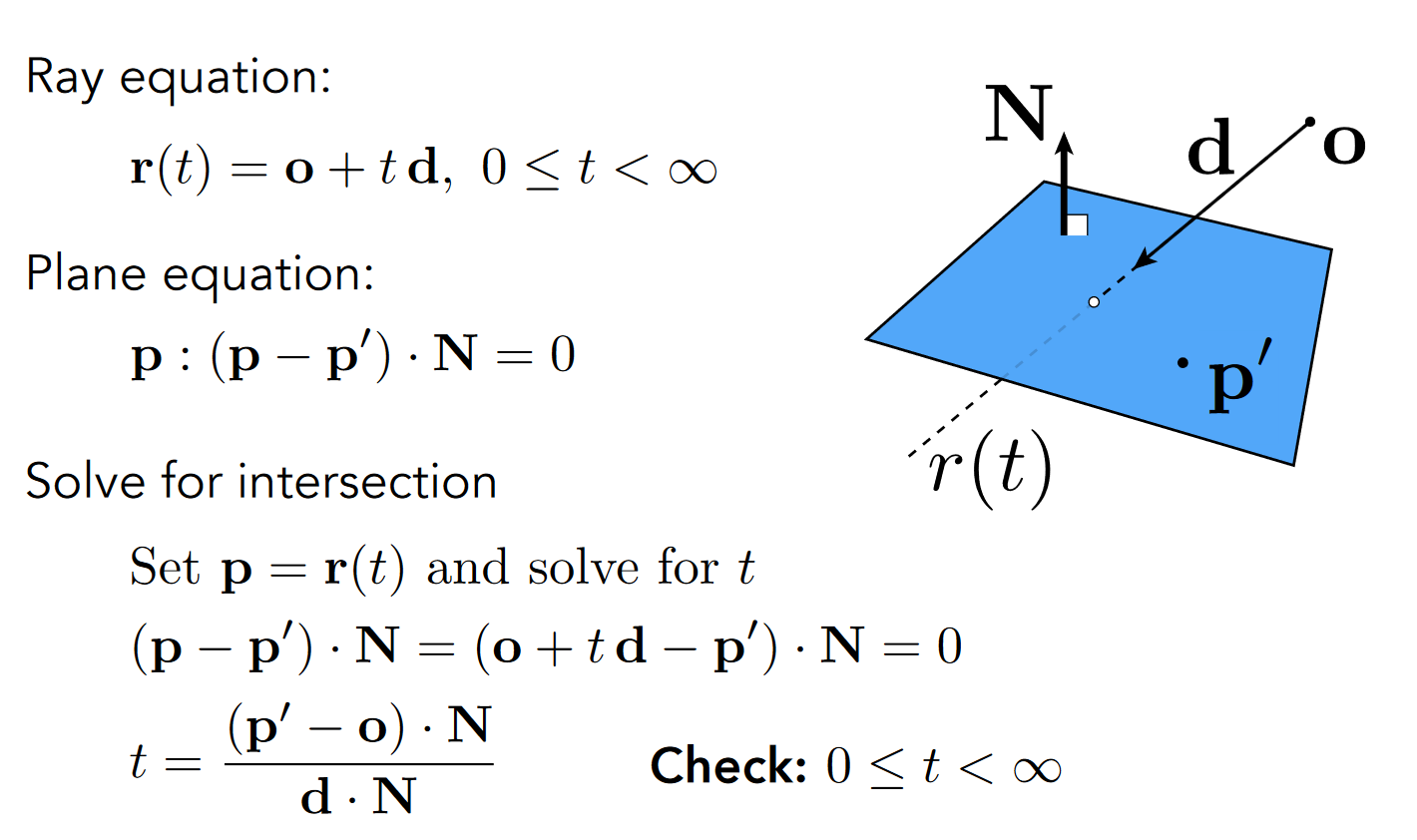
光线与三角形求交：光线与平面求交+判断交点是否在三角形内

image-20231210130304291

平面的定义：平面上一点+平面的法线

image-20231210130407893

求解交点的过程：

image-20231210130538694

Möller Trumbore Algorithm：三角形的一个点可以使用重心坐标表示

image-20231210130920469

注：解上图的方程，若$(1-b_1,b_2)、b_1、b_2$为正数，则交点在三角形内部

4.计算的加速

每个光线与全部三角形都要进行求交点的计算，会导致计算开销过大，所以需要进行计算的加速。

包围盒方法：在物体外面包一个包围盒，如果光线与盒子都没交点，那跟物体里的所有面更不会有交集。

image-20231210133306097

一般使用轴对齐包围盒（Axis-Aligned Bounding Box、AABB)

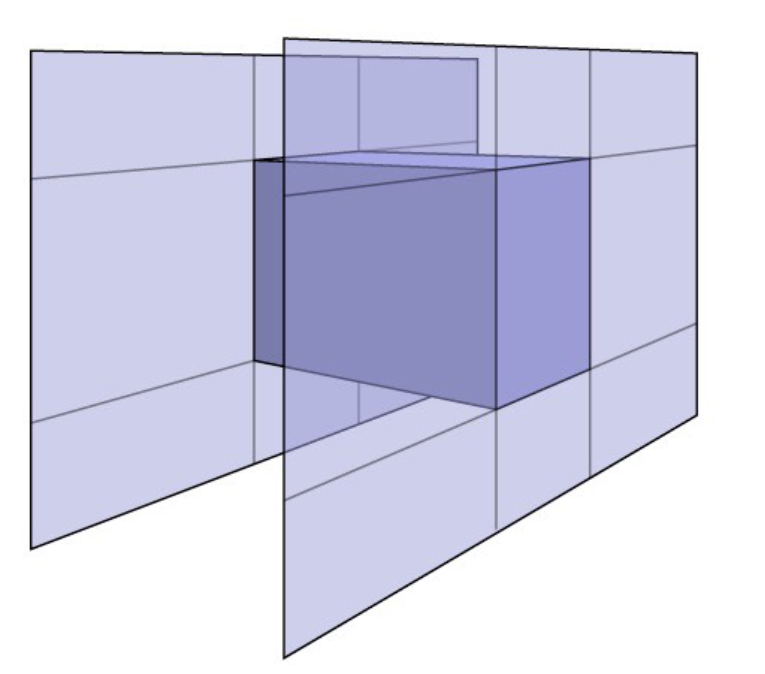
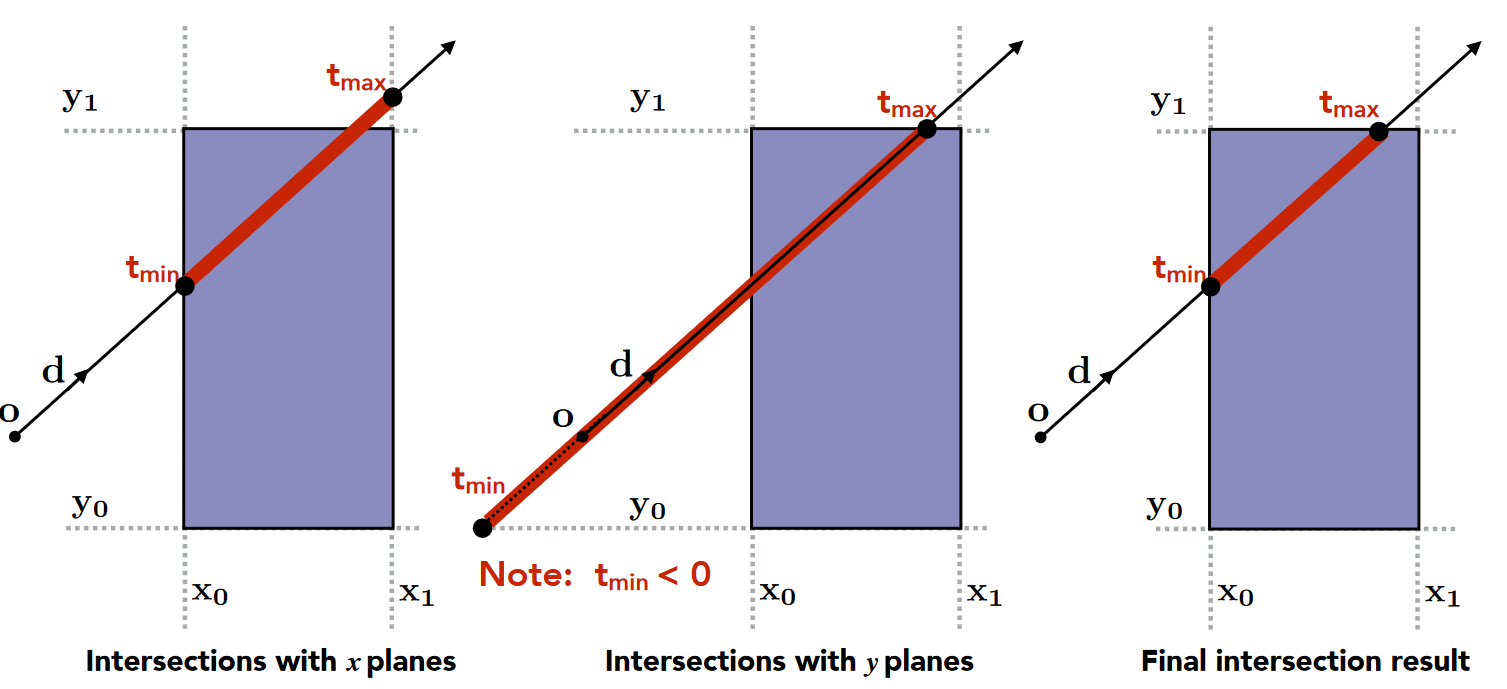
判断光线和包围盒是否有交点：通过计算光线进入/离开长方体的三个对面的时间可以判断出，光线和包围盒是否有交点

立方体有三个对面：

image-20231210133558734

进入/离开对面的时间：

image-20231210133643427

进入盒、离开盒的时间为：
image-20231210133737225

注：光线进入了三个对面则认为光线进入了盒子，而光线离开了任意一个对面，就认为光线离开了盒子。

若$t{enter}<t{exit}且t_{exit}>=0$，则有交点

注：$t_{exit}$<0，表示盒在光源背后，没有交点

5.加速结构

5.1 均匀空间划分 Uniform Spatial Partitions (Grids)

image-20231210140725279

判断光线交到的是不是含有物体表面的格子，如果不是的话跳过，是的话和其中的物体求交

注：该方法适合物体分布较均匀的场景

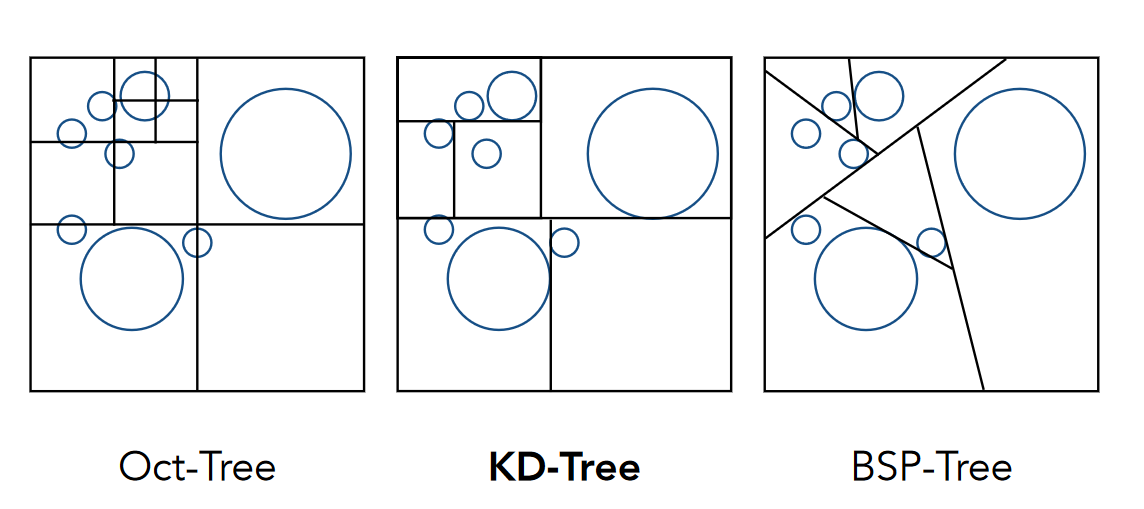
5.2 空间划分

image-20231210141331964

  • Oct-Tree:八叉树
  • KD-Tree
  • BSP-Tree

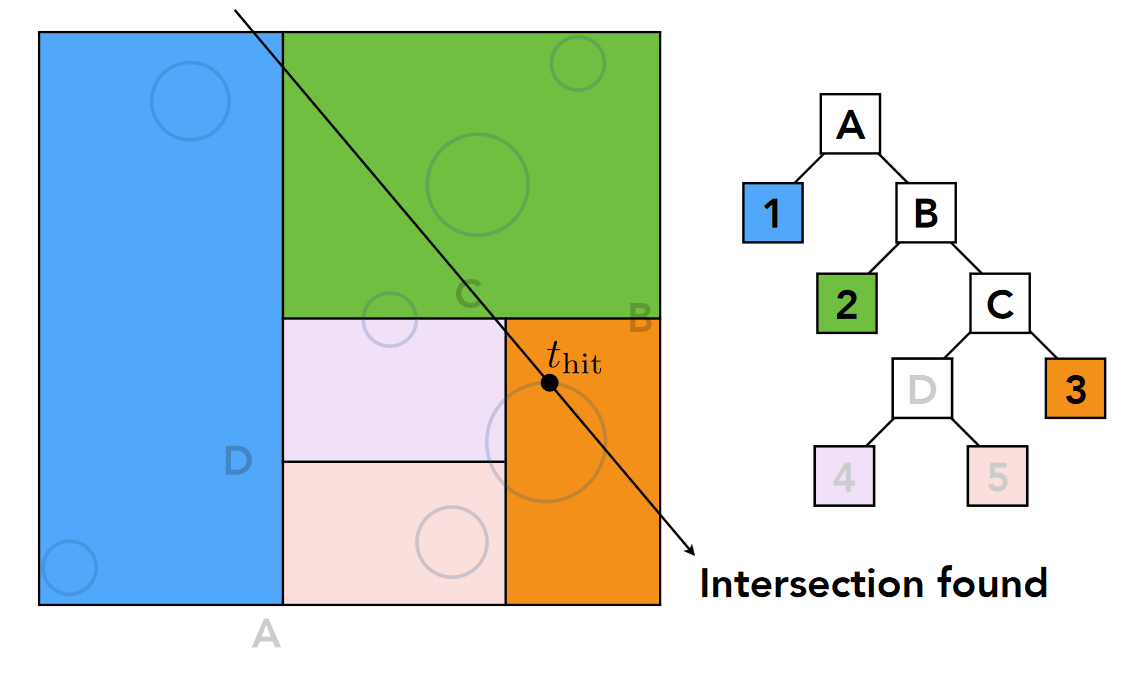
KD-Tree

image-20231210142240300

注：

1.KD-Tree中一个物体可能存在多个格子中

2.KD-Tree要计算三角形与盒子的求交，这较为困难

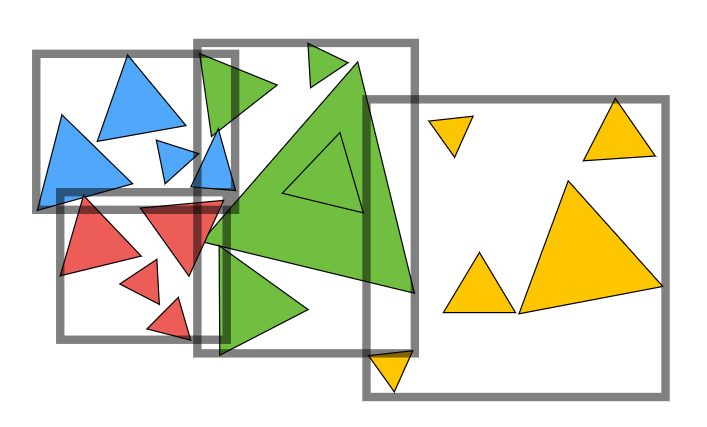
5.3 物体划分（BVH）

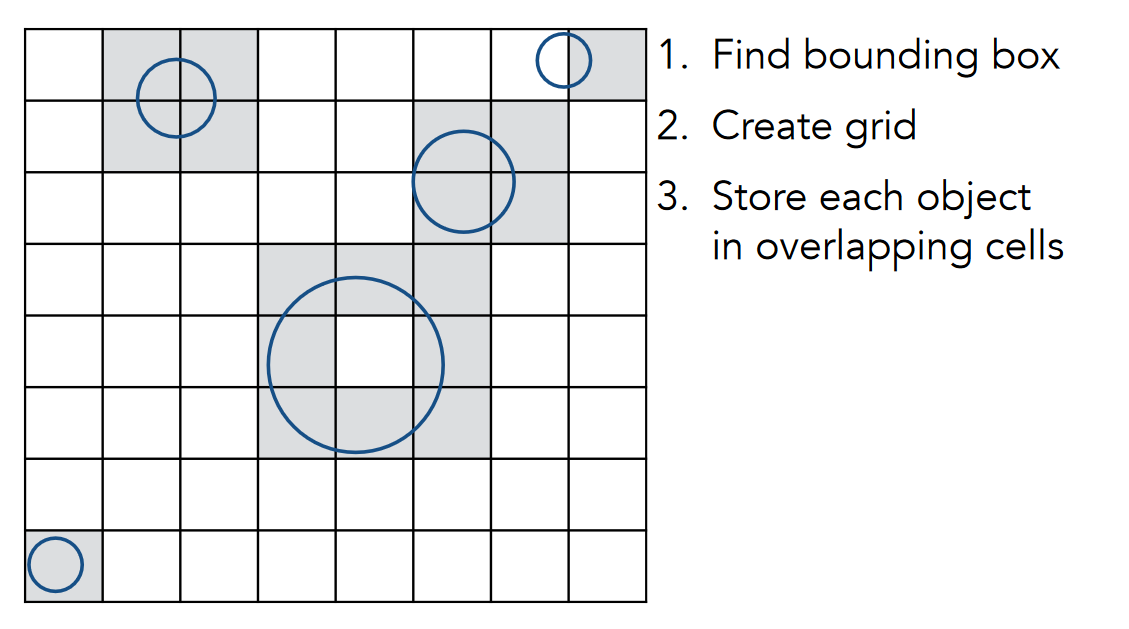
步骤：

1.找到一个包围盒

2.递归地将物体拆成两个部分

3.两个部分重新计算包围盒

4.在每个叶子节点中记录实际的物体

image-20231210143955688

注：划分规则：选择最长轴划分，以中间位置的物体进行划分