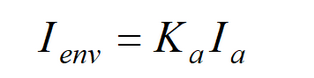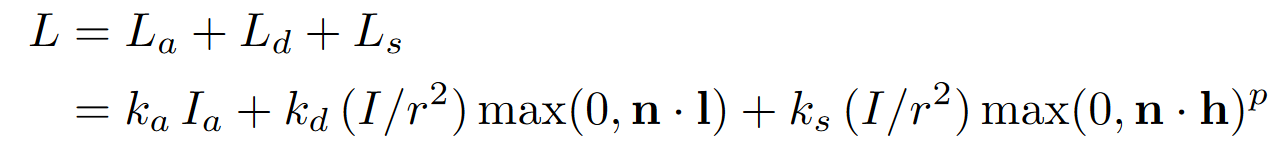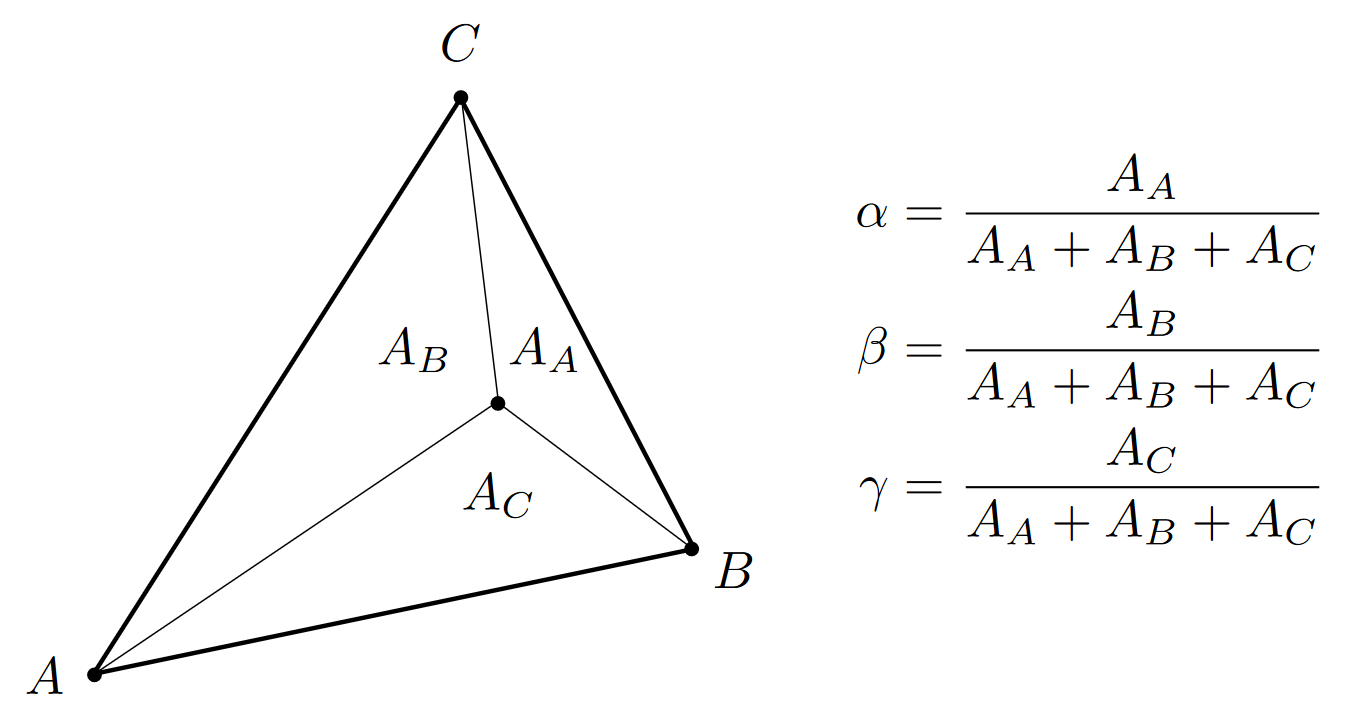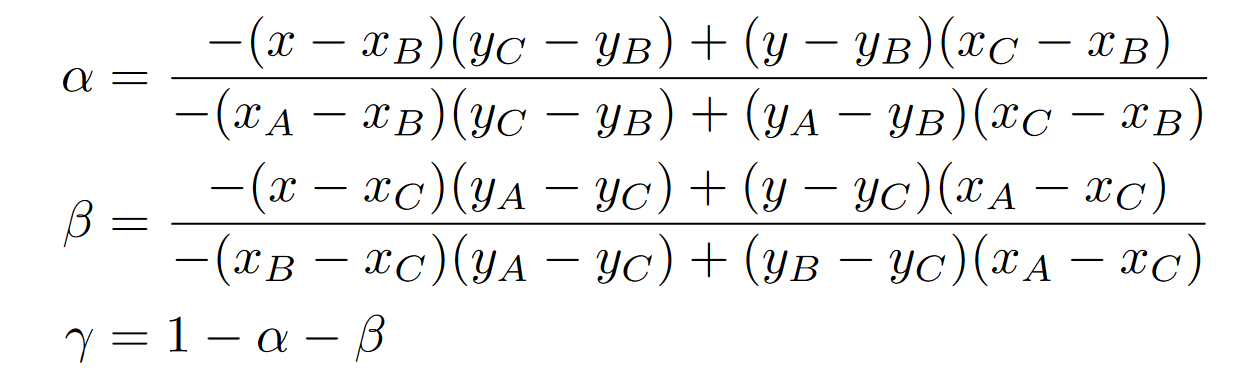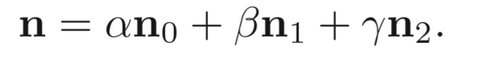局部光照模型及着色方法
1.局部光照模型
光线的简单分类:
镜面反射
漫反射
- 环境光
1.1 泛光模型
泛光模型即只考虑环境光,这是最简单的经验模型,只会去考虑环境光的影响,并且不会去精确的描述,而只是用一个简单的式子表示:
1.2 Lambert漫反射模型
在泛光模型的基础之上增加了漫反射项
- 每个不同方向反射的光的强度相等
- 产生漫反射的原因是物体表面的粗糙
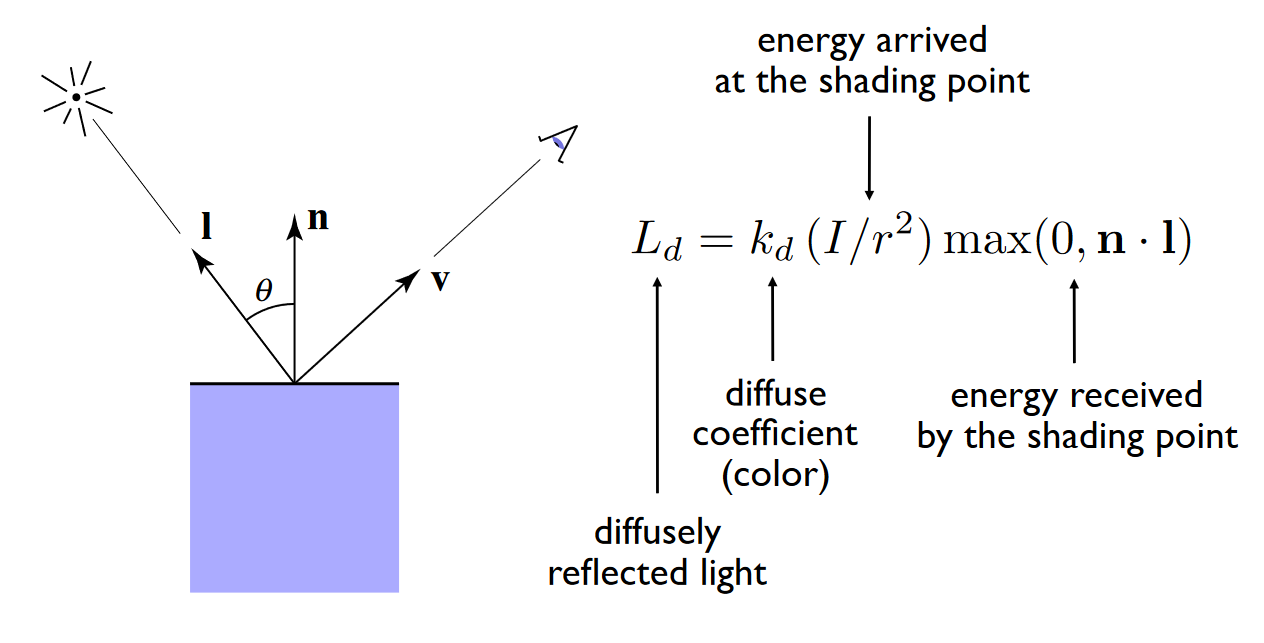
漫反射光照强度与光线照射方向和表面法线之间的夹角余弦成正比
注:漫反射与观察方向无关,光线照射方向和表面法线之间的夹角反应了对于光照的接受率
公式表示:
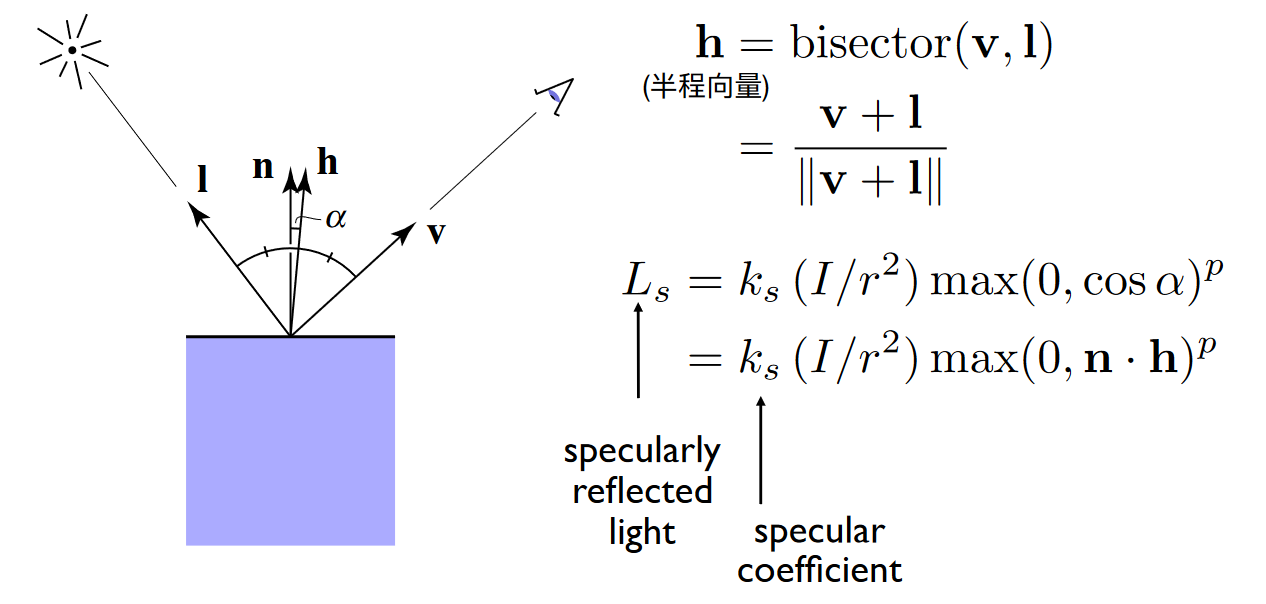
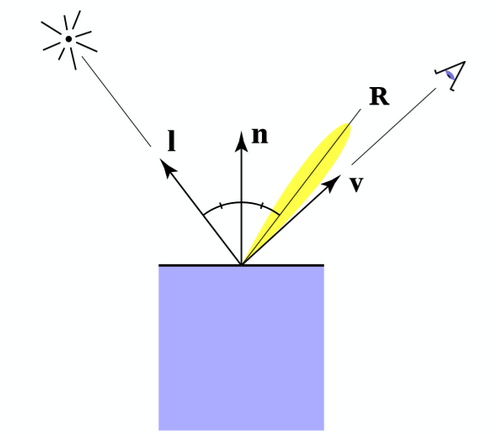
1.3 Blinn-Phong反射模型
Blinn-Phong反射模型是Phong光照模型的一种改进,在模拟高光方面表现更为自然。
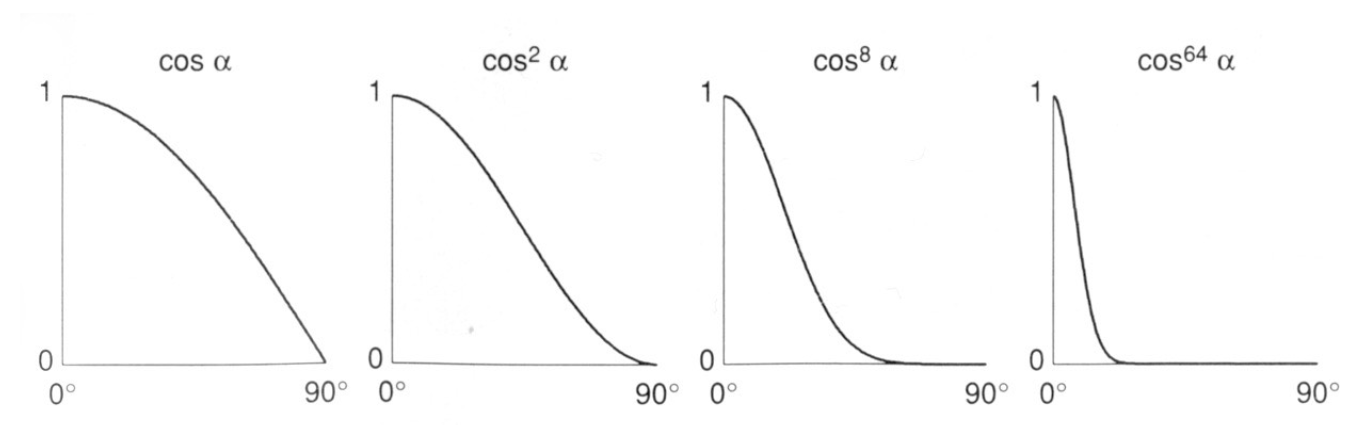
注:$k_s$为镜面反射系数, I为入射光强, r为光源到入射点距离,指数p加速衰减(用于减小可以看到高光的角度)
注:使用半程向量简化了反射向量与人眼观察夹角的计算(Phong光照模型,即下图中R与v的夹角的计算)
整体计算公式:
注:L=泛光(环境光)+漫反射项+高光
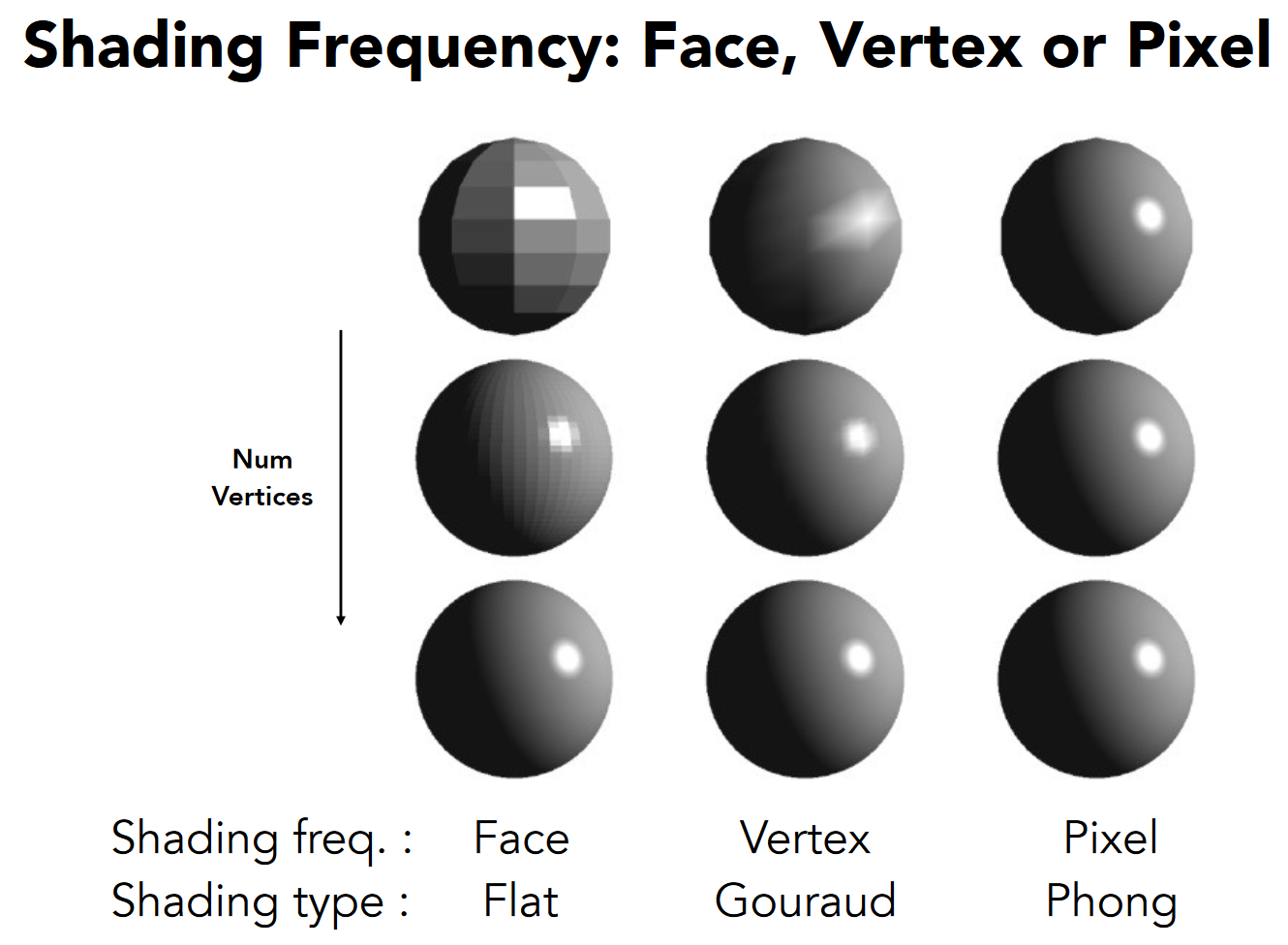
2.着色方法(频率)
2.1 Flat Shading(面着色)
模型数据大多以很多个三角面进行存储,因此也就记录了每个面的法线向量,利用每个面的法线向量进行一次Blinn-Phong反射光照模型的计算,将该颜色赋予整个面。
效果如下:
2.2 Gouraud Shading(顶点着色)
Gouraud Shading会对每个三角形的顶点进行一次着色
点法线:将所有共享这个点的面的法线向量加起来求均值,最后再标准化
三角形内部的每一个点:利用重心坐标来插值
重心坐标:给定的三角形ABC和其中的一个点P,其重心坐标$(w_a,w_b,w_c)$满足以下条件:
- $w_a+w_b+w_c=1$
- $P=w_a⋅A+w_b⋅B+w_c⋅C$
重心坐标可以通过面积的比值求出:
注:三角形的重心为(1/3,1/3,1/3),其将三角形分为了面积相等的三份。
重心坐标一般的表达式:
重心插值公式如下:
$P_{interpolated}=w_a⋅P_A+w_b⋅P_B+w_c⋅P_C$
注:$P_A、P_B、P_C$分别是三个顶点上的属性值
注:重心坐标经过投影之后可能会改变,在三维空间中插值一些属性时,要计算三维空间中重心的坐标。
2.3 Phong Shading(像素着色)
要对每个点都进行光照计算,三角形内部的每一个点的法线向量如插值颜色一样得到:
注:$n_0,n_1,n_2$分别是三角形三个顶点的法线向量,α,β,γ为三角形面内点的重心坐标